4260. НОП – 2

Найдите наибольшую общую подпоследовательность двух строк.

Вход. Две строки, состоящие только из маленьких букв английского алфавита. Длина каждой строки не превышает 1000 символов.

Выход. Выведите наибольшую общую подпоследовательность двух строк.

Пример входа	Пример выхода
abacaba dacabc	acab

РЕШЕНИЕ

наибольшая общая подпоследовательность

Анализ алгоритма

В задаче следует найти наибольшую общую подпоследовательность (НОП) двух строк и вывести ее.

Построим массив dp, где dp[i][j] равно длине НОП строк x_[1…i] и y_[1…j]. Значение dp[n][m] будет равно длине НОП исходных строк (|x| = n, |y| = m).

После вычисления массива dp восстановим НОП, совершив обратный проход по матрице dp от ячейки (n, m) до (0, 0). Для текущей позиции (i, j) выполняем следующие шаги:

· если символы x_i и y_j совпадают, этот символ должен быть включён в НОП. Добавляем его в результирующую строку res и переходим к ячейке (i – 1, j – 1), то есть продолжаем строить НОП для строк x_{[1…i – 1]} и y_{[1…j – 1]}.

· если символы x_i и y_j различны, то переходим к ячейке (i, j – 1) или (i – 1, j), выбирая ту, где значение больше. Если значения в ячейках dp[i – 1][j] и dp[i][j – 1] равны, переход возможен в любую из них.

Результирующая строка res будет содержать наибольшую общую подпоследовательность строк x и y.

Пример

Рассмотрим процесс нахождения наибольшей общей подпоследовательности (НОП) для двух строк, приведённых в примере.

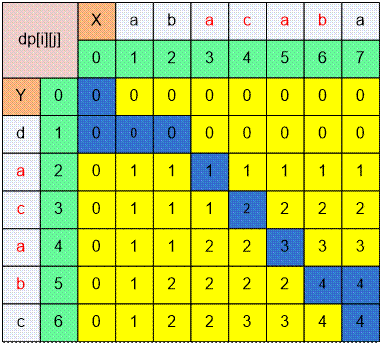
Поиск общей подпоследовательности начинается с позиции (i, j) = (6, 7).

y[6] ≠ x[7]: переходим в любую соседнюю ячейку с максимальным значением, например, в (5, 7).

y[5] ≠ x[7]: двигаемся в (5, 6).

y[5] = x[6] = ‘b’: совершаем переход по диагонали и включаем букву ‘b’ в НОП.

Реализация алгоритма

Объявим входные строки x и y. Для нахождения их НОП используем массив dp.

#define MAX 1001

int dp[MAX][MAX];

string x, y, res;

Читаем входные строки и добавляем к ним пробел спереди, чтобы индексация начиналась с 1.

cin >> x; n = x.length(); x = " " + x;

cin >> y; m = y.length(); y = " " + y;

Находим НОП.

for (i = 1; i <= n; i++)

for (j = 1; j <= m; j++)

if (x[i] == y[j])

dp[i][j] = dp[i - 1][j - 1] + 1;

else

dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);

В строке res строим НОП.

i = n; j = m;

while (i >= 1 && j >= 1)

if (x[i] == y[j])

{

res = res + x[i];

i--; j--;

}

else

{

if (dp[i - 1][j] > dp[i][j - 1])

i--;

else

j--;

}

Обращаем и выводим результирующую строку.

reverse(res.begin(), res.end());

cout << res << endl;